Mastering P-Value Calculation in Excel: A Quick Guide
Understanding and calculating the p-value in Excel can be a game-changer for researchers, data analysts, and students. It's a statistical measure that helps in hypothesis testing, indicating the strength of evidence against the null hypothesis. This guide will walk you through the process of calculating p-values in Excel, offering practical steps and insights to streamline your data analysis.
Why is P-Value Important?
Before diving into the how-to, let’s briefly look at why the p-value is significant:
- It helps in decision making regarding the null hypothesis.
- A low p-value can indicate strong evidence against the null hypothesis, suggesting that your observed data is unlikely under the null hypothesis.
- It’s used in various statistical tests like t-test, ANOVA, chi-square, and more.
Setting Up Your Excel Sheet
To calculate p-values, you’ll first need your dataset ready in Excel:
- Organize your data into columns.
- Ensure your data meets the assumptions of the test you intend to use.
🔍 Note: Ensure your data is clean and properly formatted for accurate statistical analysis.
Using Excel Functions for P-Value Calculation
Excel offers various functions to calculate p-values depending on the statistical test you’re performing:
T-Test P-Value Calculation
For a t-test comparing two groups:
- Select the data you want to compare.
- Use the function
=T.TEST(array1, array2, tails, type):- array1 and array2 are your sample data ranges.
- tails specifies whether you’re performing a one-tailed or two-tailed test (use 1 or 2).
- type indicates the test type (1 = paired, 2 = two-sample equal variance, 3 = two-sample unequal variance).
- Example:
=T.TEST(A1:A10, B1:B10, 2, 3)
ANOVA P-Value Calculation
For one-way ANOVA:
- Arrange your data into columns or rows representing different groups.
- Use Data Analysis add-in:
- Go to Data > Data Analysis > ANOVA: Single Factor.
- Input your range and click OK.
- Excel will provide the ANOVA table with p-values included.
Chi-Square Test P-Value
For a chi-square test of independence:
- Enter observed data into a contingency table.
- Use the
=CHISQ.TEST(actual_range, expected_range)function:- actual_range is your data.
- expected_range should be calculated or manually entered.

| Data | Observed | Expected |
|---|---|---|
| Group 1 | 50 | 40 |
| Group 2 | 40 | 50 |
The function would be =CHISQ.TEST(A1:B2, A3:B4).
💡 Note: Remember to verify the assumptions of each test before using the corresponding Excel function.
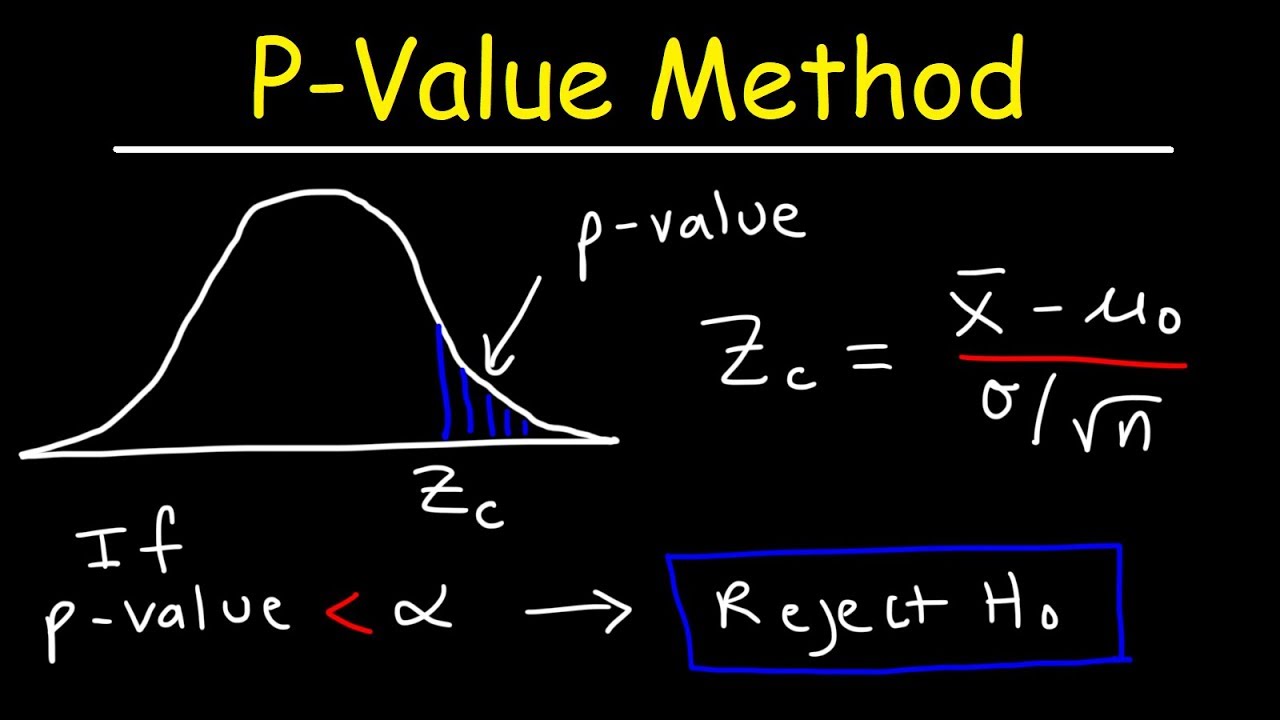
Interpreting Your P-Value
Once you have your p-value:
- Compare it with your chosen alpha level (usually 0.05 for 95% confidence).
- If p-value ≤ α, you reject the null hypothesis.
- If p-value > α, you fail to reject the null hypothesis.
The lower the p-value, the stronger the evidence against the null hypothesis. However, be cautious with very small p-values, as they can indicate extreme results or potential issues with your data.
Recap
This guide has shown you how to calculate p-values in Excel using different statistical functions:
- The t-test for comparing means.
- ANOVA for comparing multiple groups.
- Chi-square test for testing associations.
Accurate setup of data, selecting the right test, and understanding the output are critical for meaningful interpretation of p-values.
What is a p-value?
+The p-value is a statistical measure indicating the probability of obtaining test results at least as extreme as the observed results, assuming the null hypothesis is true.
Can I perform all statistical tests in Excel?
+While Excel provides functions for many common statistical tests, advanced or specialized tests might require specific add-ins or other statistical software like R or SPSS.
How do I interpret a very low p-value?
+A very low p-value (e.g., below 0.01) suggests strong evidence against the null hypothesis, meaning that the observed effect or association is very unlikely to have occurred by chance.
What if my p-value is higher than my alpha level?
+If your p-value is higher than your chosen alpha level (e.g., 0.05), you fail to reject the null hypothesis, suggesting there isn’t enough evidence to support an effect or association.
Why should I verify the assumptions of statistical tests?
+Assumptions ensure the validity of the test results. If assumptions are violated, the p-value might not accurately reflect the probability under the null hypothesis.