Z-Score Calculation Made Easy: Excel Guide
Statistics can be intimidating, but one of the most foundational tools for analyzing data distribution is the z-score. Understanding how to calculate the z-score in Microsoft Excel can transform complex statistical analysis into a task that's not only manageable but also insightful. This guide will walk you through the steps to calculate z-scores, providing practical examples, detailed explanations, and tips to ensure accuracy and clarity.
Understanding Z-Scores
The z-score, sometimes called a standard score, tells you how many standard deviations an element is from the mean. Here are the key points:
- Formula: (Z = \frac{(X - \mu)}{\sigma}) where (X) is the observed value, (\mu) is the mean, and (\sigma) is the standard deviation.
- The z-score can be positive, negative, or zero:
- A positive z-score indicates the data point is above the mean.
- A negative z-score indicates the data point is below the mean.
- A zero z-score indicates the data point equals the mean.
- It helps in normalizing data to a standard distribution, making it easier to compare different datasets.
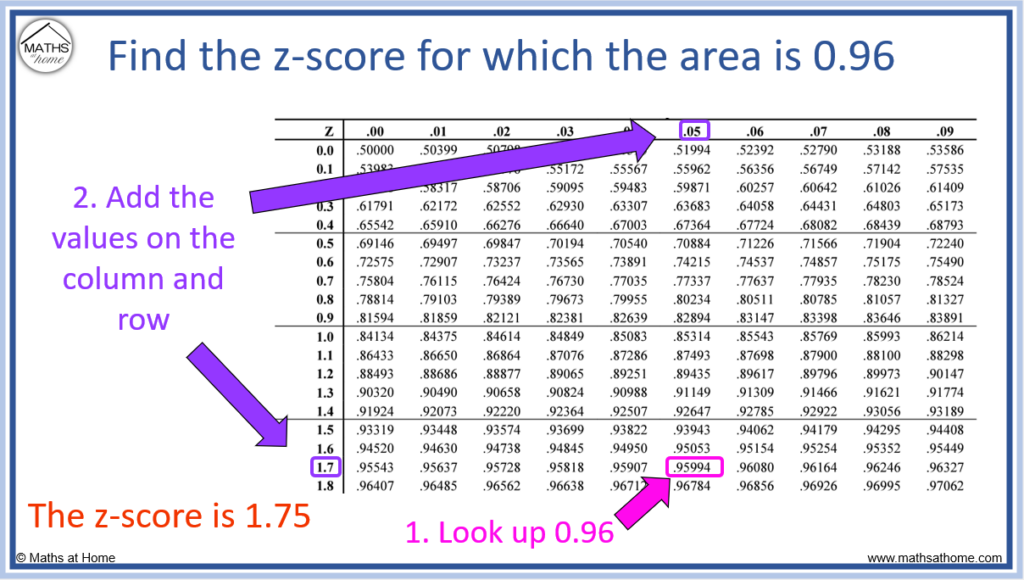
📝 Note: Understanding the distribution of your data is crucial before calculating z-scores. For normally distributed data, z-scores will follow the standard normal distribution.
Calculating Z-Scores in Excel
To calculate z-scores in Excel, you’ll need to follow these steps:
- Enter Your Data: Start by entering your dataset into an Excel sheet.
- Calculate the Mean: Use the AVERAGE function. For example, if your data is in cells A1 to A100, enter
=AVERAGE(A1:A100)in an empty cell. - Calculate the Standard Deviation: Use the STDEV.S function for a sample or STDEV.P for a population. Similarly, enter
=STDEV.S(A1:A100)or=STDEV.P(A1:A100)in another empty cell. - Calculate the Z-Score:
- In the cell where you want to calculate the z-score, subtract the mean from the data point and divide by the standard deviation. If your data is in cell B1, the mean in cell C1, and standard deviation in D1, you would use:
= (B1 - C1) / D1
Example: Calculating Z-Scores for Test Scores
Let’s say we have test scores of students as follows:

| Student | Score |
|---|---|
| Alice | 75 |
| Bob | 85 |
| Charlie | 65 |
| David | 90 |
We'll calculate the mean and standard deviation:
- Mean (μ) = 78.75
- Standard Deviation (σ) ≈ 10.31
Now, let's compute the z-scores for each student:
- Alice: (75 - 78.75) / 10.31 \approx -0.36
- Bob: (85 - 78.75) / 10.31 \approx 0.61
- Charlie: (65 - 78.75) / 10.31 \approx -1.33
- David: (90 - 78.75) / 10.31 \approx 1.09
Using Z-Scores in Excel
Here are some tips for using z-scores effectively:
- Normalization: Z-scores are useful for normalizing different datasets, allowing direct comparison despite different scales.
- Outlier Detection: Points with z-scores greater than 3 or less than -3 might be considered outliers, though this depends on context.
- Statistical Analysis: Z-scores can be used in further statistical tests or for data modeling.
📊 Note: While calculating z-scores in Excel is straightforward, always verify your data's normality before assuming standard distribution.
Closing Thoughts
The power of z-scores in statistics lies in their ability to transform raw data into a universal scale, providing insights into the variability, consistency, and anomalies within datasets. This guide has equipped you with the knowledge to calculate z-scores in Excel, leveraging this tool to make your statistical analysis more accessible and effective. Whether you’re a student, researcher, or data enthusiast, mastering the z-score calculation opens up a wealth of opportunities for data interpretation and decision-making.
What if my data isn’t normally distributed?
+While z-scores are most effective for normally distributed data, they can still be calculated for other distributions. However, the interpretation of these z-scores might differ; they won’t follow the standard normal distribution, which affects their comparative value across different datasets.
Can z-scores be used to compare scores from different tests?
+Yes, z-scores normalize scores across different distributions, making it possible to compare results from different tests or exams as long as the data’s distribution and variance are considered.
Is there a difference between z-score for a sample vs. population?
+Yes, when dealing with sample data, you use STDEV.S for calculating the standard deviation, which accounts for the fact that your sample is just an estimate of the population. For population data, you would use STDEV.P, which assumes you have all the data for the population.
Related Terms:
- probability from z score excel
- z test formula excel
- test statistic excel formula
- z score normalization excel
- example of z test
- find z score given area