5 Simple Steps to Calculate Z-Scores in Excel

When it comes to statistical analysis, Z-scores are an incredibly useful metric. Whether you're a student, a researcher, or working in data analytics, understanding how to calculate Z-scores can be pivotal for interpreting data distributions. Excel, with its widespread use and robust features, is an excellent tool for performing this calculation.

What is a Z-Score?

Before diving into the steps, let’s quickly understand what a Z-score is:

• A Z-score indicates how many standard deviations an element is from the mean.
• It shows whether an observed value is typical or an outlier in the dataset.
• Z-scores are standard, meaning they can be compared across different datasets.

Step 1: Prepare Your Data

The first step is to ensure your data is organized in Excel:

• Column A: Original Data
• Column B: Mean
• Column C: Standard Deviation

Here’s how you prepare:

1. Enter your dataset in Column A.
2. In Cell B1, calculate the mean of your dataset with the formula: =AVERAGE(A1:A[Last Row])
3. In Cell C1, calculate the standard deviation with the formula: =STDEV.P(A1:A[Last Row]) or =STDEV.S(A1:A[Last Row]) for sample data.

Step 2: Calculate the Z-Score

Now, you’ll calculate the Z-scores for each value in your dataset:

• In Cell D2, use the following formula: =(A2-B1)/C1 then drag down the column.

Here, A2 is the data value, B1 is the mean, and C1 is the standard deviation. The dollar signs ($) ensure that these cell references remain fixed as you copy the formula down.

Step 3: Interpret Your Z-Scores

Interpreting Z-scores involves understanding:

• Values closer to zero (between -1 and 1) indicate that the data point is near the mean.
• Positive Z-scores mean the data point is above the mean, and negative Z-scores indicate it’s below the mean.
• Large Z-scores (either positive or negative) signify outliers.

📊 Note: If your dataset is small, consider using the STDEV.S function instead of STDEV.P for a more accurate sample standard deviation.

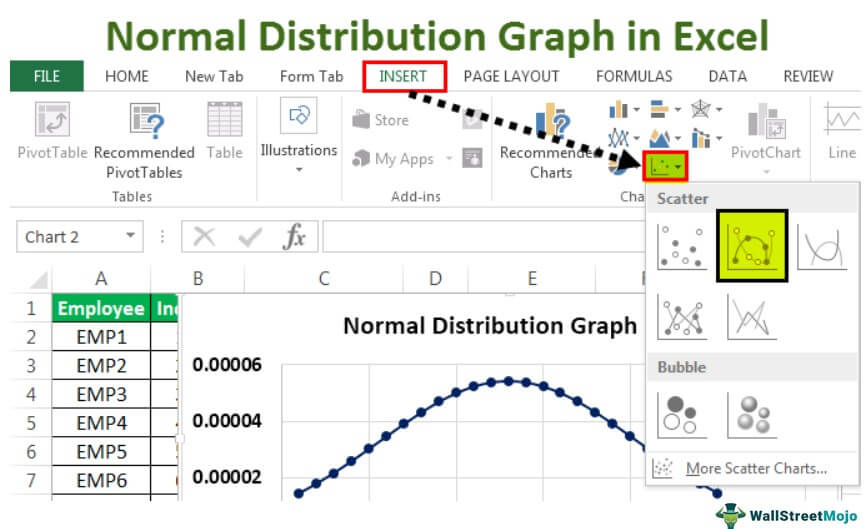
Step 4: Visualize Your Z-Scores

For better comprehension, visualizing Z-scores can be insightful:

1. Select the Z-scores column and insert a scatter plot or line chart.
2. Use a normal distribution curve for comparison:
1. Create a new column for your Z-scores from -3 to 3 in increments.
2. In another column, calculate the probability density function (PDF) for the normal distribution using the formula: =NORM.DIST([Z-score], 0, 1, FALSE)
3. Add this curve to your chart.

Step 5: Advanced Analysis with Z-Scores

Now that you have calculated and visualized your Z-scores, here’s how you can take your analysis further:

• Comparison: Compare Z-scores across different datasets or variables to see which items stand out more significantly.
• Standardization: Transform your data into Z-scores to compare different units or scales of measurement.
• Outlier Detection: Use the Z-score to determine if any data points are outliers using the general rule of thumb: Z-score > 3 or < -3 indicates an outlier.

In summary, calculating Z-scores in Excel is a fundamental skill for any data analyst. By following these steps, you can not only understand your data better but also prepare it for more advanced statistical techniques. Remember, these scores help you see beyond the raw numbers to reveal the underlying patterns in your data, providing invaluable insights into any dataset.

Related Terms:

• probability from z score excel
• z test formula excel
• test statistic excel formula
• z score normalization excel
• example of z test
• find z score given area