Calculate Cumulative Frequency in Excel Easily
In today's data-driven world, analyzing and understanding large datasets is a critical skill. One of the key statistical tools that can help us make sense of this data is cumulative frequency. This measure allows us to see how the values of a dataset accumulate over time, revealing trends, patterns, or distribution of your data. In this detailed guide, we'll delve into how you can calculate cumulative frequency in Excel with ease, making data analysis accessible for everyone, from students to professional statisticians.
What is Cumulative Frequency?
Before jumping into the technicalities, let’s define what cumulative frequency is. In statistics, cumulative frequency is the running total of frequencies. It tells you the number of observations that fall at or below a particular value in your data set. This is particularly useful in understanding:
- The cumulative proportion of data
- Trends over a distribution curve
- The percentage of data within certain ranges
Setting Up Your Excel Worksheet
Here are the initial steps to prepare your Excel worksheet for calculating cumulative frequency:
- Organize Your Data: Arrange your dataset in ascending or descending order. For simplicity, we’ll assume you’re using a vertical range of cells starting from A2 downwards.
- Create Frequency Table: In a separate column, tally how many times each value or range of values appears in your dataset.
Here’s a simple table to illustrate:

| Data | Frequency |
|---|---|
| 1 | 5 |
| 2 | 10 |
| 3 | 3 |
📚 Note: Your dataset must be sorted before creating the frequency table to ensure accuracy in the cumulative frequency calculation.
Calculating Cumulative Frequency
With your data and frequency table prepared, here’s how to calculate cumulative frequency in Excel:
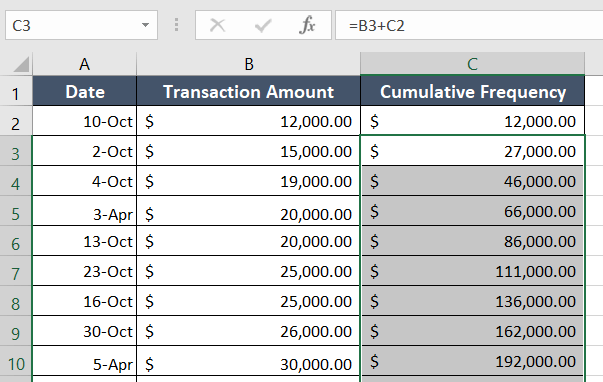
- Enter Formula: In the first row of your cumulative frequency column, which could be labeled as “Cumulative Frequency” in cell C2, enter the formula:
- Auto Fill: Drag the bottom right corner of cell C2 down to autofill the formula in the remaining cells. This will:
- Use the value from the frequency column for the first entry.
- Sum the value from the previous cumulative frequency with the current frequency for subsequent entries.
=B2
Here’s an example of how your spreadsheet might look:
| Data | Frequency | Cumulative Frequency |
|---|---|---|
| 1 | 5 | =B2 |
| 2 | 10 | =B3+C2 |
| 3 | 3 | =B4+C3 |
💡 Note: Ensure your data is clean and free from outliers, as these can skew your cumulative frequency calculations.
Interpreting Cumulative Frequency Results
After calculating the cumulative frequency, you’ll want to interpret these results:
- Patterns and Trends: Look at how the frequency accumulates to identify peaks, troughs, or plateaus in your data distribution.
- Percentile Calculations: With cumulative frequencies, you can easily calculate percentiles or understand what percentage of data falls within certain ranges.
Visual representation can also enhance your understanding:
- Create a Cumulative Frequency Histogram or Ogives for a graphical representation.
In our wrap-up, understanding how to calculate and interpret cumulative frequency can provide valuable insights into your data. This tool is especially useful for those looking to gauge the distribution of their data, understand trends over time, or perform detailed statistical analyses.
The ability to use Excel for these calculations not only streamlines the process but also empowers users to make data-driven decisions with confidence. As you explore further, consider the following frequently asked questions for additional clarity.
Why is it important to sort data before calculating cumulative frequency?
+Sorting data ensures that cumulative frequency calculations are accurate and understandable, as they build upon the previous data points sequentially.
Can I calculate cumulative frequency for grouped data?
+Yes, the principle remains the same; you would calculate the frequency of each group and then sum these for the cumulative total.
How can cumulative frequency help in decision making?
+Cumulative frequency can reveal distribution patterns, help in understanding percentiles, and guide decision-making by providing insights into data accumulation over time or categories.