Calculate P-Value in Excel Easily - Quick Guide

Introduction

Calculating the p-value in Excel can often feel like a daunting task, especially if statistics isn’t your strong suit. However, Excel offers several straightforward methods to compute p-values, which can help you determine the statistical significance of your data. This guide will walk you through these methods, ensuring that you can quickly and accurately assess your research findings or any statistical hypotheses.

What is P-Value?

The p-value is a fundamental concept in statistics that helps in hypothesis testing. It represents the probability of observing an effect at least as extreme as the one in your sample data, assuming that the null hypothesis is true. Here’s a brief overview:

• Definition: The p-value measures the probability that a result is due to chance.
• Interpretation: A lower p-value indicates that your results are less likely due to random chance, thus supporting your alternative hypothesis.
• Typical Threshold: Many research fields consider a p-value of less than 0.05 as evidence to reject the null hypothesis.

Method 1: Using T.DIST.RT

If you have a t-statistic from a two-tailed test, you can calculate the p-value using the T.DIST.RT function:

1. Enter your t-statistic in a cell (e.g., A1).
2. Use the formula =T.DIST.RT(A1, degrees of freedom). For example, if your t-statistic is in A1 and your degrees of freedom are 10, the formula would be =T.DIST.RT(A1, 10).

📝 Note: Ensure the degrees of freedom are correctly specified as this will influence your p-value significantly.

Method 2: Using Normal Distribution

For large sample sizes where you can approximate your test statistic to a normal distribution, you can use the following:

1. Calculate your test statistic (e.g., z-score).
2. Use Excel’s NORM.S.DIST function to find the p-value: =NORM.S.DIST(A1, TRUE), where A1 contains your z-score. Here, TRUE returns the cumulative distribution function, giving you the probability below the z-score, which you can then double for a two-tailed test.

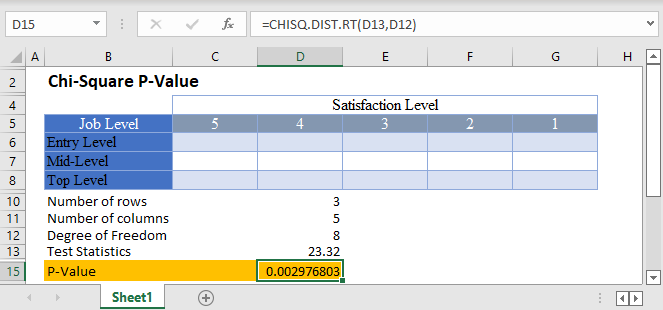
Method 3: Chi-Square Test

If you’re dealing with categorical data or testing for independence or goodness-of-fit, use:

1. Compute your Chi-Square test statistic.
2. Enter the statistic in a cell (say A1).
3. Use the function =CHISQ.DIST.RT(A1, degrees of freedom).

Method 4: ANOVA

For comparing means of more than two groups, Analysis of Variance (ANOVA) can be used:

1. Set up your data in columns, each column representing a different group.
2. Use Excel’s Data Analysis Toolpak to perform ANOVA:
   • Go to Data > Data Analysis > Anova: Single Factor.
   • Input your data range and set your significance level.
   • Excel will output an ANOVA table with an F-statistic and p-value.

Interpreting Your P-Value

Once you have your p-value:

• If the p-value is less than your chosen significance level (commonly 0.05), you reject the null hypothesis.
• If it’s greater, you fail to reject the null hypothesis, suggesting that the observed effect could be due to chance.
• The smaller the p-value, the stronger the evidence against the null hypothesis.

Understanding and accurately calculating the p-value in Excel allows researchers, students, and analysts to make data-driven decisions with confidence. This guide has outlined several methods to compute p-values for different statistical tests, ensuring that you can handle various scenarios in your statistical analysis. Whether you're testing for differences in means, association in categorical data, or variance among multiple groups, Excel provides the tools to perform these calculations efficiently. Always remember to interpret your p-value within the context of your research and consider effect sizes and practical significance alongside the statistical significance.