Calculating P-Values with Excel: Quick Guide
Understanding the significance of results in data analysis is critical for making informed decisions. In this context, P-values serve as a vital statistical tool, helping to assess the strength of evidence against the null hypothesis. This guide will walk you through the process of calculating P-values using Microsoft Excel, a software commonly used for statistical computations due to its accessibility and ease of use.
Understanding P-Values
Before we dive into the Excel specifics, let's define what a P-value is:
- P-value represents the probability of observing results at least as extreme as those in your data, assuming the null hypothesis is true.
- A lower P-value indicates stronger evidence against the null hypothesis, often leading to its rejection in favor of the alternative hypothesis.
Step-by-Step Guide to Calculating P-Values in Excel
Excel offers several functions that can be employed to calculate P-values for various statistical tests. Here, we'll focus on the most common scenarios:
1. For T-Tests
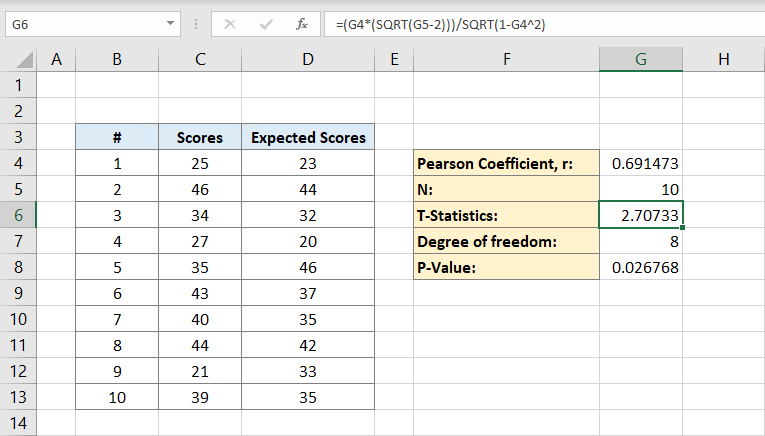
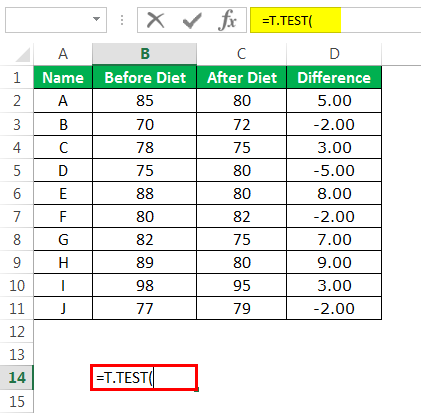
When comparing means from two samples or conditions, T-tests are the go-to method. Here's how to calculate a P-value for a T-test:
- Calculate the t-statistic manually or use the `T.TEST` function.
- Use the T.DIST or T.DIST.2T function to find the P-value:
- For a one-tailed test: `=T.DIST.2T(t-statistic, degrees of freedom)`
- For a two-tailed test: `=T.DIST(t-statistic, degrees of freedom, TRUE)`

🔍 Note: Remember to adjust the degrees of freedom correctly. For a two-sample T-test, it's typically `n1 + n2 - 2`, where n1 and n2 are the sample sizes of the two groups.
2. For Chi-Square Tests
To assess the relationship between categorical variables:
- Set up your contingency table.
- Use the CHISQ.TEST function: `=CHISQ.TEST(actual_range, expected_range)`
- The returned value is the P-value.
3. For Anova
Analysis of Variance (ANOVA) is used to compare means across multiple groups:
- Arrange your data with groups in columns or rows.
- Use Data Analysis Toolpak or calculate manually:
- Calculate the F-statistic.
- Use the F.DIST function to find the P-value: `=F.DIST(f-statistic, numerator_df, denominator_df, TRUE)`
Common Pitfalls When Calculating P-Values
Here are some pitfalls to avoid:
- Using the wrong distribution: Make sure your test assumptions align with the distribution you choose.
- Incorrect degrees of freedom: This can lead to incorrect P-values.
- Neglecting sample size: Larger samples can detect smaller differences, potentially skewing your P-value.
Interpreting P-Values
Once you've calculated your P-value, interpreting it correctly is key:
| P-value Range | Interpretation |
|---|---|
| < 0.01 | Strong evidence against the null hypothesis |
| 0.01 - 0.05 | Moderate evidence against the null hypothesis |
| 0.05 - 0.10 | Weak evidence against the null hypothesis |
| > 0.10 | Little to no evidence against the null hypothesis |
With these guidelines, you can navigate through the process of calculating P-values in Excel effectively. While Excel offers robust tools for statistical analysis, it's essential to approach this task with a clear understanding of the statistical tests involved and the correct application of Excel functions.
The journey from data to decision-making is fraught with complexity, but by mastering the calculation and interpretation of P-values, you empower yourself to make data-driven decisions confidently. Remember, the P-value is just one tool in the statistical toolbox; always consider other metrics and the broader context of your data to draw meaningful conclusions.
What if my P-value is greater than 0.05?
+If your P-value is greater than 0.05, there is not enough evidence to reject the null hypothesis. This might suggest that the observed effect could be due to chance, but remember that this threshold is somewhat arbitrary and should be considered in the context of your study.
Can Excel perform advanced statistical tests?
+Yes, Excel can perform a variety of statistical tests through its built-in functions and add-ins like the Analysis Toolpak. However, for very complex analyses or large datasets, specialized statistical software like R or SPSS might be more appropriate.
Why do I need to know the sample size when calculating P-values?
+Sample size affects the power of your test. Larger samples increase the chances of detecting smaller differences as statistically significant, which in turn influences the P-value. Calculating P-values correctly requires understanding the degrees of freedom, which is directly related to sample size.
Related Terms:
- excel correlation p value
- find p value using excel
- p value t test excel
- getting p value in excel
- formula for p value
- p value error in excel