5 Simple Ways to Calculate Uncertainty in Excel
Why Excel is the Ultimate Tool for Calculating Uncertainty
Excel is a widely recognized software tool known for its robust capabilities in data analysis, calculations, and visualization. Whether you're a student, researcher, or business professional, Excel can streamline your analysis with functions specifically designed to handle uncertainties in datasets. Here’s why Excel excels at this task:
- Versatility: Excel can manage various types of data from different sources, making it adaptable for multiple scenarios.
- Extensive Functions: With functions like AVERAGE, STDEV, and more, Excel provides tools to estimate uncertainty with precision.
- Visualization: Beyond calculations, Excel helps in graphically representing uncertainty through charts, aiding in data interpretation.
- Automation: Formulas can automatically update with new data, reducing human error and saving time.
⚠️ Note: Always ensure your data is clean and organized before starting calculations in Excel to avoid errors.
Method 1: Using the AVERAGE and STDEV Functions
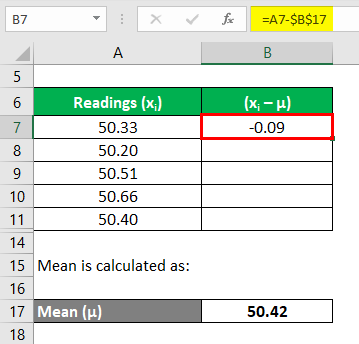
The AVERAGE and STDEV functions are foundational for assessing central tendencies and variability in your dataset.
- AVERAGE: Calculates the mean of the selected range.
- STDEV: Computes the standard deviation, which is a measure of the dispersion of data points from the mean.
Here’s how to use them:
- Enter your data into an Excel spreadsheet.
- To calculate the average, use
=AVERAGE(A2:A10)if your data is in cells A2 through A10. - To find the standard deviation, use
=STDEV(A2:A10).
Example:

| Observations | Data |
|---|---|
| Data 1 | 12.3 |
| Data 2 | 15.6 |
| Data 3 | 9.8 |
| … | |
| Average | =AVERAGE(A2:A10) |
| Standard Deviation | =STDEV(A2:A10) |
💡 Note: If you're dealing with the entire population, use STDEVP instead of STDEV.
Method 2: Error Propagation in Excel
When combining measurements with inherent uncertainties, error propagation allows you to calculate the uncertainty of the resultant value. Excel can help with this through simple mathematical operations:
- Addition/Subtraction: The combined uncertainty is the square root of the sum of squared uncertainties.
- Multiplication/Division: The uncertainty percentage is the square root of the sum of squared percentage uncertainties.
For example:
| Measurement 1 | Value | Uncertainty |
|---|---|---|
| Length (A) | 20 | 0.5 |
| Width (B) | 15 | 0.3 |
| Area (A * B) | =A2*B2 | =SQRT(((C2/A2)^2+(C3/B2)^2)*D2) |
🔍 Note: Ensure the cell references for the uncertainty calculation formula correspond to your spreadsheet setup.
Method 3: Monte Carlo Simulation for Complex Uncertainties
Monte Carlo simulation offers a probabilistic approach to uncertainty estimation, which is particularly useful when dealing with multiple variables or non-linear relationships. Here's how to implement it in Excel:
- Define your variables and their respective uncertainties.
- Create a simulation to randomly sample within these uncertainties.
- Calculate the desired outcome for each simulation.
- Summarize the results using statistical functions to understand the distribution.
Here's an example of a simple Monte Carlo simulation in Excel:
=MORATORIO.MCSim(D2, E2, F2, G2, 10000)
🧭 Note: Monte Carlo Simulation can be computationally intensive. Consider Excel's processing power and your data size when applying this method.
Method 4: Sensitivity Analysis
Sensitivity analysis examines how the uncertainty in the output of a model can be apportioned to different sources of uncertainty in the model's inputs. In Excel, this can be achieved by varying one input variable at a time and observing the changes in the output:
- Set up your base case model in Excel.
- Adjust one variable at a time to see how the results change.
- Plot or tabulate these changes to understand sensitivity.
Here's a basic example of a sensitivity analysis table:
| Input Variable | Value Range | Output Result |
|---|---|---|
| Variable 1 | 5 to 15 | Calculated Result |
| Variable 2 | 20 to 30 | Calculated Result |
Method 5: GUM Uncertainty Framework
The Guide to the Expression of Uncertainty in Measurement (GUM) provides a standardized approach for quantifying measurement uncertainty. Excel can implement this through several steps:
- Identify all sources of uncertainty.
- Quantify each source using statistical analysis.
- Combine uncertainties using the law of propagation of uncertainty.
- Report the results with standard uncertainty and an expanded uncertainty estimate.
To apply this in Excel:
| Source | Value | Standard Uncertainty |
|---|---|---|
| Measurement Error | =STDEV(A2:A10)/SQRT(COUNT(A2:A10)) | |
| Calibration Uncertainty | Input Calibration Uncertainty | |
| Environmental Conditions | Input Environmental Uncertainty | |
| Total Uncertainty | =SQRT(SUM(C2:C4^2)) |
🛑 Note: The GUM framework is standardized but requires thorough understanding for correct implementation.
In summary, Excel is a versatile tool for calculating uncertainty, offering various methods like the AVERAGE and STDEV functions, error propagation, Monte Carlo simulations, sensitivity analysis, and the GUM framework. Each method provides a different level of complexity and insight into data uncertainties. By mastering these techniques, you can confidently quantify uncertainties in your data, enhancing the reliability of your analysis.
What is the difference between STDEV and STDEVP functions?
+STDEV calculates the standard deviation for a sample, whereas STDEVP calculates the standard deviation for the entire population. Use STDEVP when your dataset represents the whole population to avoid bias in the estimate of variability.
How many simulations should I run for a Monte Carlo analysis?
+The number of simulations depends on your computational resources and the desired precision. Typically, 10,000 to 100,000 simulations are sufficient for most applications to achieve a stable distribution.
Can Excel handle GUM uncertainty calculations for complex models?
+While Excel can perform basic GUM calculations, for complex models, specialized uncertainty calculation software might be more suitable. However, Excel’s flexibility allows it to be used for straightforward applications with proper setup.
What are some common sources of uncertainty?
+Common sources include measurement errors, instrument calibration, environmental conditions, operator variability, and the model used for data interpretation.
Is it necessary to perform uncertainty calculations for every data analysis?
+No, not every analysis requires uncertainty calculations. It depends on the context and the level of precision needed. However, for scientific research, engineering, and high-precision applications, uncertainty quantification is crucial.
Related Terms:
- formula to calculate uncertainty
- measurement uncertainty calculation examples
- uncertainty calculator excel free download
- formula to find uncertainty
- calculate measurement uncertainty in excel
- how to calculate mean uncertainty